リー微分と保存則について

エネルギー運動量テンソルの保存則について書こうと思ったのだけど、リー微分を説明してからじゃないと説明できない。

ネーターの定理はまたに書く。とりあえず、エネルギー運動量テンソルの保存則まで書く。

リー微分でネーターの定理と保存則について説明が書いてあるのは、
WaldのGeneral Relativityで
APPENDIX C　Maps of Manifolds, Lie Derivatives, and Killing Fields
APPENDIX E Lagrangian and Hamiltonian Formulation of Einstein Equations
だ。

Lie微分について、ちょっと詳しく書いてから、エネルギー運動量テンソルの保存則について書いてみようと思う。

相対性理論での空間はリーマン多様体だ。

多様体というのは、ざっくばらんに言うと局所的に座標が書ける空間のことを言う。相対性理論で重要なのは、局所的座標が書けることから接空間TpM(速度場が定義できる)を定義することができ、さらにその双対空間である余接空間Tp*M、さらにテンソル空間が局所的に定義できることである。

今回に必要なのは、多様体であるってことだけ。

さらに、相対性理論では、

接空間　余接空間　テンソル空間に計量を与えて、局所的にノルム(長さ)を決める。計量を与えた多様体をリーマン多様体という。
そして、リーマン接続(計量を保存し、れい率テンソル=0)が入る。

しかし、今回はあまり関係ない。

さて、ひとつ仮定を置く。

物理量は局所的に定義されたテンソル量である。

この原理は十分局所であれば、重力のない空間(局所慣性系)とみなせる座標系をとることができるという要請から導かれる。これをもう少し強めて、局所的な空間はローレンツ対称性があるとすると、その表現の分類からテンソル量だけではなく、スピノール場などを得ることができる。まぁ、一応書くと

物理量は局所的な値をもち、ローレンツ対称性を満たす。

一応これで、リー微分を語る舞台が整った。

さて、ここからはしばらく数学の話。

空間をMとNとする。MとNは別の空間だけど、後で同一の空間とみなす。

M上の点をmとし、それをN上の点nに移す写像をfとする。
$f:M \ni m \rightarrow q=f(n) \in N$

この写像の微分dfは、TmMの元vを、TnNの元wに移す。
$f_* = df:TmM \ni v \rightarrow w=df(v) \in TnN$

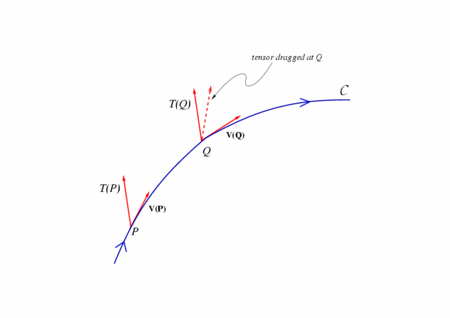
ナンクルさんの図を拝借*1

まぁ、こういうこと。詳しいことは、多様体の基礎p234(微分同相写像とベクトル場でも)

ここで、 $f_*$ がfの向きと同じ対応である。こういうのを共変関手という。圏が出てきた(^^)

また、fは引き戻し
$f^*:Tn*N \ni \omega \rightarrow \nu=f^*\omega \in Tm*M$
を誘導する。 $f^*$ の向きはfと反対。こういうのを反変関手という。
ここで、 $f^*$ は
[tex:=<\omega,f_*v>]
で定義する。ここで
[tex:=\delta^i_j]

またM上に定義された関数φをfで移すときは、
$f^*:G(N)\ni \psi \rightarrow \phi=f^* \psi \in F(M)$
を
$f^* \psi=\psi(f(m))$
で定義する。これも同様に反変関手になっている。

こうやって、ベクトル(0,1)、スカラー(0,0)、一形式(1,0)に対してfの誘導写像を定義することができた。

混合テンソルに対しては自然な誘導写像を一般には定義することができないが、fが微分同相写像であるとき、つまりM=Nのときは混合テンソルに関して自然な誘導写像f_*を定義することができる。

証明
M=Nより、反変関手 $f^*$ は、逆写像 $(f^*)^-1$ をもつので、たとえば、(1,1)型の混合テンソルをとおいたときに
$f_* : T^1_1(M) \ni f_*(T^\mu_\nu \frac{\partial }{ \partial x^\mu} \otimes dx^\nu ) \rightarrow T^\mu_\nu (\frac{ \partial y^\alpha}{ \partial x^\mu})(\frac{\partial x^\nu}{ \partial y^\beta})\frac{\partial}{ \partial y^\alpha} \otimes dy^\beta \in T^1_1(N)$
で(1,1)型の混合テンソルの共変関手 $f_*$ を定義すればよい。

てなことで、M=Nの場合には、混合テンソルについて誘導写像を定義することができた。

さて、いよいよリー微分について。

M上の点を $\phi_t:p \rightarrow q=\phi_t(p)$ で移すことを考える。これは1変数変換群と呼ばれている。
ここでφはさっきまでfと呼んでたもの。
物理的には流れによって粒子が運ばれていると考えてもよい。
参考http://people.sissa.it/~rezzolla/lnotes/virgo/node7.html

これを微分すれば速度場vが得られる。
Lie微分とは、テンソルTに対して、
$L_v=\frac{(\phi_{-t})_* T_{\phi_{t}(p)}-T_p}{t}$
で定義される。

これで、やっとリー微分が定義できた。定義をみればわかるように接続とかの概念はない。

ここで、れい率=0の条件を使うと、
$L_v T^{a_1,\cdots a_k}_{b_1,\cdots b_l}=v^c \nabla_c T^{a_1,\cdots a_k}_{b_1,\cdots b_l}-T^{a_1,\cdots a_k}_{b_1,\cdots b_l}\nabla_c v^{a_i}+T^{a_1,\cdots a_k}_{b_1,\cdots b_l}\nabla_{b_j}v^c$
が言える。

共変微分はおまけみたいなもの。

うーんと、ネーターの定理の前に

エネルギー運動量テンソルについて

最小作用の原理というものがある。
注意：場をφで書き、一変数変換群を $\sigma_\lambda$ と書く。

すべての場φはローレンツ群の表現によって分類できる。しかしここではテンソルだけにする。

最小作用の原理とは、

場φが与えられた時に、φとそのφの一回微分だけから構成されるスカラー密度関数Lagrangian $L(\phi,\partial_i \phi)$ が与えられ、それを空間積分した作用 $S=\int L \sqrt{-g}dtd^3x$ が最小となるときが場の運動を記述する

という原理だ。

さて、 $\sigma_\lambda$ は空間上の点を一斉に移す写像だと考えよう。 $\sigma_\lambda$ の写像がM上の点すべてに定義できていればなんでも良い。簡単のため考察している領域が一つの座標系 $(t,x^1,x^2,x^3)$ で覆えているとする。一番簡単なのは、回転や並行移動だろう。

作用Sが $\sigma_\lambda$ に対して不変であるとは、
$\int_U L(\phi(p))\sqrt{-g(p)}dtd^3x=\int_{\sigma_\lambda U} L(\sigma_\lambda_* \phi(p))\sqrt{-\sigma_\lambda_* g(p)}dtd^3x$
であることをいう。ここで、 $\sigma_\lambda U$ は $\sigma_\lambda$ によって移された領域のこと。

L(p)√-g(p)のときL(q)√-g(q)をと全領域について積分していくのだが、十分広い領域をとれば、同じものについて積分しているだけなので、当然成り立つ。微小座標変換ということもある。

これから、
$0=lim_{\lambda \rightarrow 0} \frac{1}{\lambda}\left({\int_{\sigma_\lambda U} L(\sigma_\lambda_* \phi(p))\sqrt{-\sigma_\lambda_* g(p)}dtd^3x-\int_U L(\phi(p))\sqrt{-g(p)}dtd^3x}\right)$
が言える。さらに $\sigma_\lambda U \cup U \subset W$ とし、境界で0であることを仮定すると
$0=L_v \int_{W} L(\phi(p))\sqrt{-g(p)}dtd^3x$
つまり
$0=\int d^4 x L_v (L(\phi(p))\sqrt{-g(p)})$
が導かれる。
$0=\int d^4 x\left(\frac{\partial L(\phi)\sqrt{-g}}{\partial \phi}-\partial_i \frac{\partial L(\phi)\sqrt{-g}}{\partial_i \phi}\right)L_v \phi + \left(\frac{\partial L(\phi)\sqrt{-g}}{\partial g_{jk}}-\partial_i \frac{\partial L(\phi)\sqrt{-g}}{\partial_i g_{jk}}\right)L_v g_{jk}$
となる。

場φが最小作用の原理を満たしているときは、第一項は消える。
よって、
$0=\int d^4 x \left(\frac{\partial L(\phi)\sqrt{-g}}{\partial g_{jk}}-\partial_i \frac{\partial L(\phi)\sqrt{-g}}{\partial_i g_{jk}}\right)L_v g_{jk}$
となる。

ところで、 $L_v g_{jk}$ について
$L_v g_{jk}=v^c\nabla_c g_{jk} + g_{ck}\nabla_j v^c + g_{jc}\nabla_k v^c$
$= \nabla_j v_k + \nabla_k v_j$
の関係がある。

また、
$T^{jk}=-\frac{2}{\sqrt{-g}}\left(\frac{\partial L(\phi)\sqrt{-g}}{\partial g_{jk}}-\partial_i \frac{\partial L(\phi)\sqrt{-g}}{\partial_i g_{jk}}\right)$
とおけば、
$0= -\frac{1}{2} \int d^4 x T^{jk}(\nabla_j v_k + \nabla_k v_j) \sqrt{-g}$
$= -\int d^4 x T^{jk} \nabla_j v_k \sqrt{-g}$
$= -\int d^4 x \nabla_j (T^{jk} v_k)- (\nabla_j T^{jk}) v_k \sqrt{-g}$